Blog
Quantum Processors Model the Flow of Information in Complex Materials
Algorithmiq, in collaboration with IBM, Flatiron Institute, EPFL, and the University of Ljubljana
Richard Feynman’s 1981 insight — that quantum systems should be used to simulate other quantum systems — has guided four decades of scientific effort.
Here, we describe an experiment that realizes this vision in a physically meaningful regime: using a Heron IBM processor, we have modeled operator dynamics in heterogeneous quantum materials, revealing information-flow patterns beyond the reach of classical computation.
The model, designed and theoretically studied by Algorithmiq, demonstrates how structured disorder shapes transport, localization, and entanglement.
The results, benchmarked against state-of-the-art tensor-network methods, including techniques from Flatiron Institute and EPFL, inaugurate an openly verifiable era of useful quantum advantage.
In 1981, Feynman asked whether a classical computer could efficiently simulate quantum mechanics.
He concluded that it could not — the number of variables required grows exponentially with system size — and proposed instead a new kind of computer that “obeys quantum laws.”
Four decades later, that question has evolved.
Rather than seeking abstract proofs of “quantum supremacy,” today’s researchers aim to demonstrate useful quantum advantage: cases where quantum hardware yields physically meaningful insight that no known classical method can reproduce.
At Algorithmiq we have designed one of the most flexible and programmable models to simulate quantum systems capturing regions of different degrees of complexity, including cases that defy all state-of-the-art classical computational methods attempted so far.
In his 1981 speech, “Simulating Physics with Computers,” Richard Feynman says: “Nature isn’t classical, dammit, and if you want to make a simulation of Nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem, because it doesn’t look so easy.” Complex materials like the Algorithmiq’s models of heterogeneous structures on the left, are hard to simulate classically but currently available quantum computers are capable of doing that with proper algorithms.
Modelling the Messiness of Matter
Real materials are rarely uniform. They contain defects, strain, impurities, and interfaces — features that make them heterogeneous. In such systems, transport is no longer smooth: some regions conduct rapidly, others trap or scatter excitations. This structured disorder underlies the behaviour of catalysts, solid-state batteries, and quantum magnets, yet it remains exceptionally difficult to model.
—
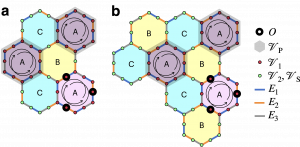
This figure clarifies the problem of operator hydrodynamics in materials. Graph structure \( (V,E) \) of the heterogeneous material defines scrambling (\(U_1\)) and unscrambling (\(U_2\)) evolutions—a combination of which manifests in the destructive interference effects—that are hard to capture with the classical methods. The difference between U1 and U2 in the overall dynamics \(U^* = U_2^* U_1\) for an observable O (originally landing on vertices VO) is in the presence of scattering on some of the vertices (VS) or the edges (ES) in \(U_2^*\). The physical question is to probe how much of the operator density is located in the geometric area VP (marked by a question mark “?”) as a result of the eventual operator spreading \(U^* O U\).
—
In the experiment that Algorithmiq’s team designed and the IBM’s team conducted, the IBM’s heavy-hex-topology quantum processor (in the left top corner of the figure) effectively functions as a programmable quantum metamaterial [N. I. Zheludev and Y. S. Kivshar, From metamaterials to metadevices, Nature materials 11, 917 (2012)]— a synthetic medium whose microscopic structure and couplings can be engineered at will. By introducing spatially varying interactions, we create a landscape where information flows, localizes, or interferes much like in real heterogeneous solids. The resulting dynamics evoke parallels with Kitaev materials [S. Trebst and C. Hickey, Kitaev materials, Physics Reports 950, 1 (2022),], whose bond-dependent interactions produce rich patterns of entanglement and fractionalization. Bridging these two ideas, the heavy-hex lattice of qubits becomes both an engineered metamaterial and a quantum simulator of emergent matter.
Operator Hydrodynamics — A Field Theory of Information Flow
In conventional hydrodynamics we describe conserved quantities such as energy or charge. In operator hydrodynamics, the quantity that “flows” is information: the geometrical operator density whose flow is dictated by an underlying (generally time dependent) Hamiltonian dynamics.
If \(O(0) \) is a local operator at time \(t = 0\), its evolved form is \( O(t) = U^\dagger (t) O(0) U(t),\) where \(U(t) = exp(−iHt).\)
The rate at which O(t) spreads — quantified through its operator weight distribution and the effective support of the geometrical operator density — encodes how quickly the system scrambles information.
In uniform lattices, this spreading forms a light-cone structure.
In heterogeneous lattices, the cone deforms, leading to patchy, anisotropic transport.
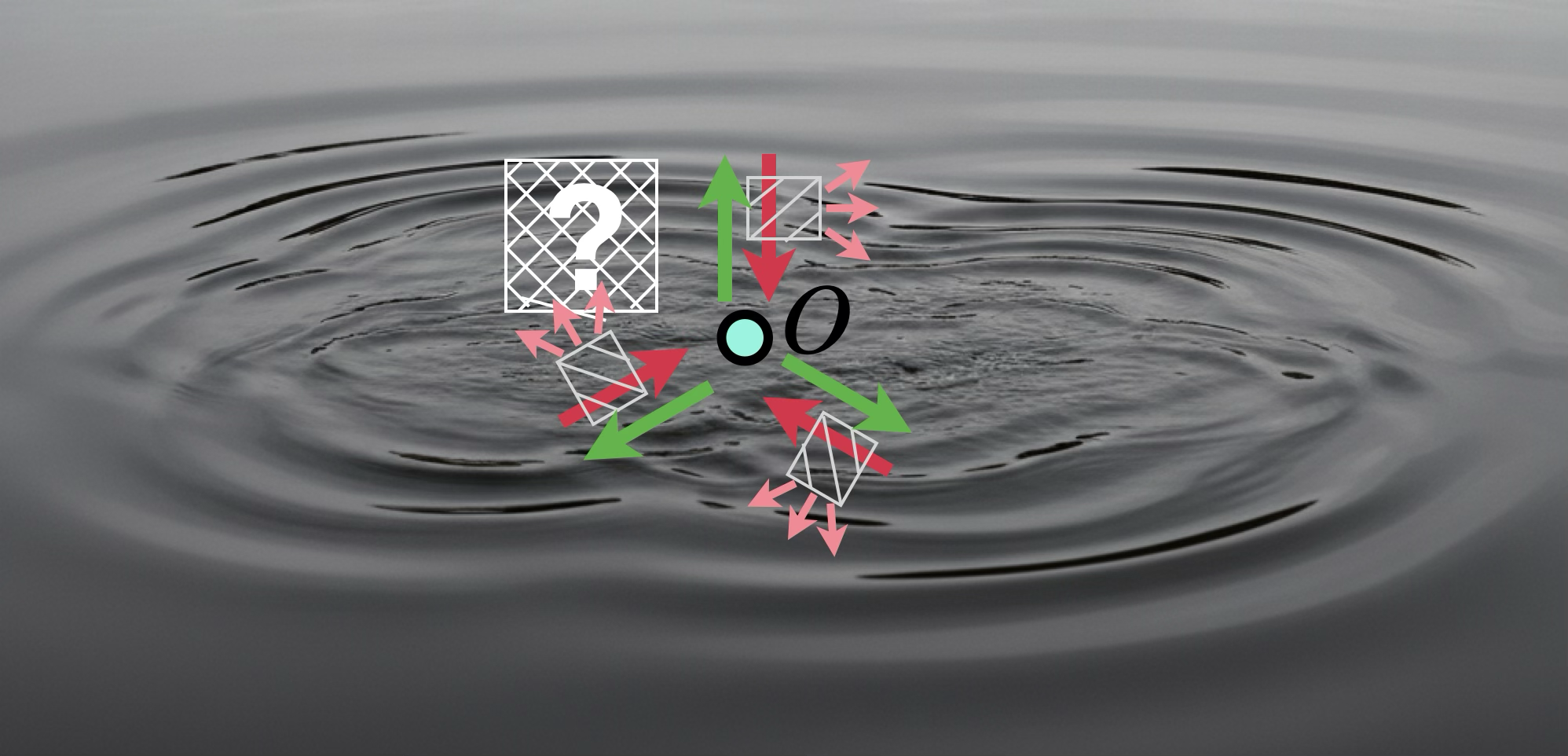
The flow of geometrical operator density in the heterogeneous structures resembles the complex (non-concentric) propagation of ripples on a water surface, with the interference effects and scattering (pink arrows) affecting the direction and the intensity of information spreading. The problem of operator hydrodynamics that we address in the experiment is to measure the integral operator density located in the chosen geometric area, for instance, one marked by a question mark “?”.
The Operator Loschmidt Echo — Watching Quantum Ripples Return
The figure of merit for the integral operator density (located in a specific geometric area) is the infinite-temperature out-of-time-order correlation function (OTOC) \(Tr( [G, U^* O U]^* [G, U^* O U] ) \) for the generator G acting nontrivially in the area. OTOC is probed with the operator Loschmidt echo (OLE) signal \(Tr [U V\delta U^* O U Vδ^* U^* O]\) with \(V\delta = exp(-I \delta G)\). It is the OLE measurement and the OTOC extraction that lies at the heart of the algorithmic part of the experiment.
—
Algorithmiq’s design of the quantum experiment intended to probe the operator hydrodynamics with the operator Loschmidt echo and out-of-time-order correlation functions. Observable O consits of Z operators in the area VO. Preparation of a randomly chosen bitstring-state. Evolution of the state under \(U V\delta U^*\) results in the output that can be measured in the computational basis. Averaging the parity of the input bitstring times the observable estimation provides the OLE estimation and its statistical error.
—
To probe this spreading experimentally, the collaboration used the operator Loschmidt echo, a quantity sensitive to reversibility.
Two nearly identical evolutions are performed: one forward under U, one backward under \( U(\delta) = U exp(−I\delta G)\), where \(\delta\) controls a small local perturbation generated by G.
The echo amplitude is
\(A(\delta) = \langle O | U^\dagger (\delta) U | O\rangle\),
serves as the operator autocorrelation.
\(A(\delta) = 1\) implies perfect reversibility; decay of \(A(\delta)\) reveals how information disperses and entangles.
This experimental protocol, sometimes called a perturbed mirror circuit, allows direct measurement of operator spreading — effectively transforming a quantum processor into a microscope for information flow.
The OTOC can be extracted from the OLE as the following figure explains.
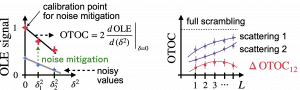
Left: Extraction of OTOC from OLE signals for different values of \(\delta\). Global rescaling of the noisy signals with respect to that for \(\delta=0\) is the simplest noise-structure-agnostic error mitigation technique; however, there exist other noise-aware methods such as the tensor-network error mitigation (TEM, patented by Algorithmiq) that rely on the learnt structure of the noise and should provide a confidence interval for the mitigated values. Importantly, all error-mitigation techniques have a calibration point at \(\delta=0\) since the whole circuit reduces to a mirror circuit. Right: Revealing the physics of scattering. L quantifies the number of Floquet layers in \(U_1\) and \(U_2\). Full scrambling assumption poses the upper bound for OTOC, \(2|VP|\). Scattering on different elements of the structure (regimes 1 and 2) results in different OTOC values. The difference \(\delta\)OTOC between those OTOCs in reasonably shallow circuits is challenging for all known classical methods.
Algorithmiq’s Theoretical Model
Algorithmiq designed and theoretically characterized the heterogeneous model underlying the experiment.
In the first experiment, qubits are arranged on a heavy-hex lattice, the same topology native to IBM processors. However, the model is adjustable to arbitrary topologies, for instance, square-lattice one that is naturally compatible with Google’s, IQM’s, Rigetti’s computers. Any material topology can be also simulated with the help of reconfigurable Quantinuum’s, QuEra’s, and IonQ’s quantum computers. Algorithmiq’s family of models is universal and allows to work with all routinely native entangling gates: models with the continuously parameterized RZZ-like and Mølmer-Sørensen-like native entangling gates, models with the CX- and CZ-like native entangling gates, models with the RXX+YY and iSWAP-like native entangling gates.
Rather than treating this geometry as a hardware constraint, Algorithmiq exploits it as a materials-design feature.
By assigning different local coupling strengths (fast and slow links), the team has engineered a synthetic material with regions of distinct dynamical behaviour — a programmable analogue of structured disorder.
The effective Hamiltonian takes the form
\( H = \sum_{⟨u,v⟩} J_{uv} Z_u Z_v + \sum_i B_i Z_i + \sum_i X_i, \)
where \(J_{uv}\) and \(B_i\) vary across the lattice.
Fast sites (red) have larger J and B values; slow sites (green) smaller ones.
This non-uniformity introduces frustration and mixed coordination numbers, key ingredients for complex transport.
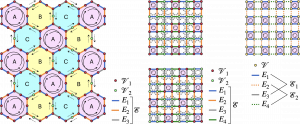
Example topologies the Algorithmiq’s family of models is compatible with.
Experimental Realization on IBM’s Heavy-Hex Processor
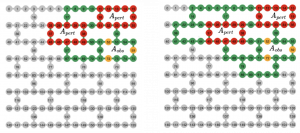
Heavy-hex topologies probed in the IBM’s experiment: (a) 49 qubits, (b) 70 qubits.
—
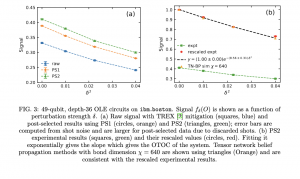
The experiment was executed on IBM’s 49-qubit heavy-hex device. Each run implemented the mirror-circuit sequence \(U_1 \rightarrow U_2 (\delta) \rightarrow U_1^\dagger \rightarrow U_2^\dagger (\delta) \).
For \(\delta = 0\) the sequence ideally returns the system to its initial state (\(A = 1\)).
By varying \(\delta\), the team measured how \(A(\delta)\) decays — the signature of operator spreading.
Error mitigation was applied to correct readout and gate errors, producing a fidelity-weighted signal \( A( \delta ) \approx A_{exp(\delta)}/A_{exp(0)}\).
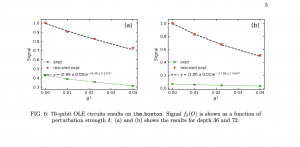
Data were collected for system sizes up to L = 6 loops (49 and 70 qubits).
Classical Benchmark and Breakdown
To assess classical limits, teams at Flatiron Institute and EPFL simulated the same circuits using advanced tensor-network such as belief-propagation algorithms.
These methods approximate the quantum state as a network of tensors with finite bond dimension χ.
For small L, both quantum and classical results coincide.
As L increases, entanglement entropy grows and the bond dimension χ required for accurate results simply explodes; convergence fails beyond \(L \approx 4\).
This divergence establishes a quantitative boundary where classical resources scale exponentially while quantum hardware continues to operate with a reasonable error-mitigation overhead.
On one hand, the tensor-network methods struggle due to the compression errors caused by the high entanglement generated in either of \(U_1\) and \(U_2\). The tensor-network methods are also limited in the bond dimension in the attempt to accurately capture the combined evolution operator \(U^* = U_2^* U_1\) in the from-the-middle-out contractions. The fast contraction method based on the belief propagation is approximate in non-tree tensor networks due to the loop correlations. On the other hand, the Pauli-propagation-like methods struggle due to the limited memory for tracking the operator branching and merging during the destructive interference.
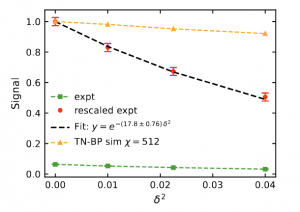
Plot with the IBM’s experimental results for the 70-qubit experiment and comparison against the belief-propagation tensor-network methods.
Information Hydrodynamics in Heterogeneous Media
Analysis of the data reveals spatially non-uniform operator dynamics.
Fast regions exhibit rapid scrambling — the local echo decays quickly — whereas slow regions retain memory, creating “cold zones” of partial localization.
This emergent pattern mirrors phenomena observed in real materials, such as sub-diffusive transport and mobility edges in disordered conductors.
The heavy-hex lattice, with its combination of geometric frustration and mixed connectivity, therefore functions as a synthetic quantum material whose transport properties can be tuned at will.
This dual identity — computer and material — exemplifies the convergence of quantum information and condensed-matter physics.
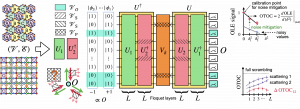
Algorithmiq’s pipeline to study information hydrodynamics in heterogeneous media.
Defining Progress: From Moment to Interval
Historically, computing milestones have been recorded as single points: the fastest supercomputer, the largest model, the first quantum supremacy claim.
But in quantum science, progress is better described as an interval — a period during which quantum hardware achieves results unattainable by any classical means.
When classical algorithms eventually catch up, the interval closes and a new one begins.
This moving boundary defines a dialogue between the two paradigms, not a declaration of victory.
Open Verification and the Quantum Advantage Tracker
To ensure transparency, the results of this demonstration will appear in IBM’s Quantum Advantage Tracker, a publicly accessible platform that records verified quantum and classical benchmarks side by side.
By hosting experimental data, simulation scripts, and error-mitigation protocols, the Tracker transforms quantum advantage from a static claim into an evolving, community-verified process.
“We are no longer chasing a single moment of quantum advantage,” says Sabrina Maniscalco, CEO of Algorithmiq. “We are building an experiment that never really ends — one that invites the entire community to explore where the classical ends and the quantum begins.”
Implications for Materials and Devices
Understanding operator hydrodynamics in heterogeneous systems has broad consequences:
– Catalysis: maps how electronic correlations localize near active sites.
– Solid-state batteries: reveals percolation and blocking pathways for ionic transport.
– Organic photovoltaics: models exciton diffusion and energy-funneling efficiency.
– Quantum devices: informs design strategies to localize or slow error propagation.
By learning to control information flow, researchers can design materials and architectures that exploit, rather than avoid, disorder — turning complexity into functionality.
Future Benchmarks
The collaboration plans a sequence of increasingly complex challenges:
– Spin transport in frustrated magnets — probing thermalization and entanglement propagation.
– Adaptive quantum chemistry (benzene benchmark) — extending Algorithmiq’s TEM algorithms for correlated molecules.
– Exciton transport in organic photovoltaics — linking quantum dynamics to light-harvesting efficiency.
Each benchmark will appear in the Tracker, defining successive intervals of quantum advantage and expanding the frontier of the computable.
Toward a Unified Science of Computation
This experiment demonstrates that quantum hardware is becoming a general-purpose platform for programmable quantum matter.
It fulfills Feynman’s original prediction not as a philosophical statement but as a working scientific method.
The operator Loschmidt echo on a heterogeneous lattice is more than a computation; it is an observation of physics that no classical experiment or algorithm could replicate.
In doing so, it redefines what “simulation” means — merging hardware, theory, and material behavior into a single, self-consistent experiment.
Author
Sergei Filippov
Senior Researcher
Sabrina Maniscalco
CEO